More Information
Submitted: May 27, 2024 | Approved: June 17, 2024 | Published: June 18, 2024
How to cite this article: Saeed EF. Utilizing a Visual Method, Focuses on the Modeling of the Semi-empirical Mass Formula "SEMF" in Nuclear Physics. J Radiol Oncol. 2024; 8: 051-054.
DOI: 10.29328/journal.jro.1001064
Copyright License: © 2024 Saeed EF. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Binding energy; Nuclide tabletop; Semi-empirical mass equation; Nuclear science; 3D printers; Modeling; Film
Utilizing a Visual Method, Focuses on the Modeling of the Semi-empirical Mass Formula "SEMF" in Nuclear Physics
Esraa Fareed Saeed*
Department of Science, Physics and Earth Sciences Curriculum Division, General Directorate of Curriculum, Ministry of Education, Iraq
*Address for Correspondence: Esraa Fareed Saeed, Department of Science, Physics and Earth Sciences Curriculum Division, General Directorate of Curriculum, Ministry of Education, Iraq, Email: israaphysics200684@gmail.com
An empirical framework that accurately describes radioactive bonding energies is the somewhat empirical mass equation (SEMF). They showcase many implementations and uses of the idea that rely on graphics and printed objects. A key new addition is a contrast with real experiments, as well as a visualization of the energy environment as supplied by the SEMF. The shortcomings of the empirical theory are shown by our visualization of this differential energy scenery, which also highlights the significance of what are known as magic numbers—an explanation provided by the outermost approach, which was developed much more recently than the water drop theory. This provides a great chance to talk about the advantages and limitations of simulations everywhere within the framework of science teaching.
Nuclear science is a fundamental area of study in contemporary physics, with many pertinent implications such as radioactive decomposition and nuclear Fusion and division. In the Karlsruhe, Germany Nuclid Chart and the Brookhaven, Maryland National Laboratory’s Diagram of Elements, both of which are accessible on the internet, isotopic elements with varying numbers of neutrons N are listed as a generalization of the periodic structure of factors, categorized as aspects according to the amount Z of electrons [1,2].
An essential component of scientific learning is the clear explanation of the function of simulations in the universe, and in particular, the capacity to talk about the boundaries of concepts [3]. Examining the precision of the water drop paradigm and, consequently, the SEMF in atomic physics appears to be a favorable chance to address the function of theories in modern science. Furthermore, the three-dimensional dynamic environment of the binding forces per nucleotide EB (Z, N)/A may be shown with the use of contemporary digital animation. In fact, a variety of approaches of visualizing the forces that bind have been put out recently, including some that make use of graphics and movements found in well-known video games like Minecraf [4].
In these contributions, we expand on this research in two ways: first, we employ the technology of 3D printing to create easily reproducible sensory representations for decay of radioactive material and binding forces per nucleus in the classroom [5,6]. Together with the 3D-printed approach, we also created a film that contrasts the SEMF’s forecasts with real empirical information to illustrate the model’s fundamental beliefs as well as their relationship to the mystical numbers and the exterior model. We discover novel representations of the differential energy terrain that highlight the significance of known mystical numbers and expose the shortcomings of the experiential model, particularly for tiny isotopes.
According to the 1949 Goeppert-Mayer and Jensen nuclear envelope approach, protons are especially robust when the neutron and proton counts match the ideal figures. It is noteworthy that enchantment numbers could have been predicted from the simpler fluid drop model, despite the fact that these numbers were described considerably later than the SEMF [7].
When combined, the models may be utilized in the classroom to thoroughly examine significant nuclear physics subjects as well as to promote thinking critically about model construction in contemporary economics as a whole [8].
Through the enchanted numbers to the somewhat empirical mass equation
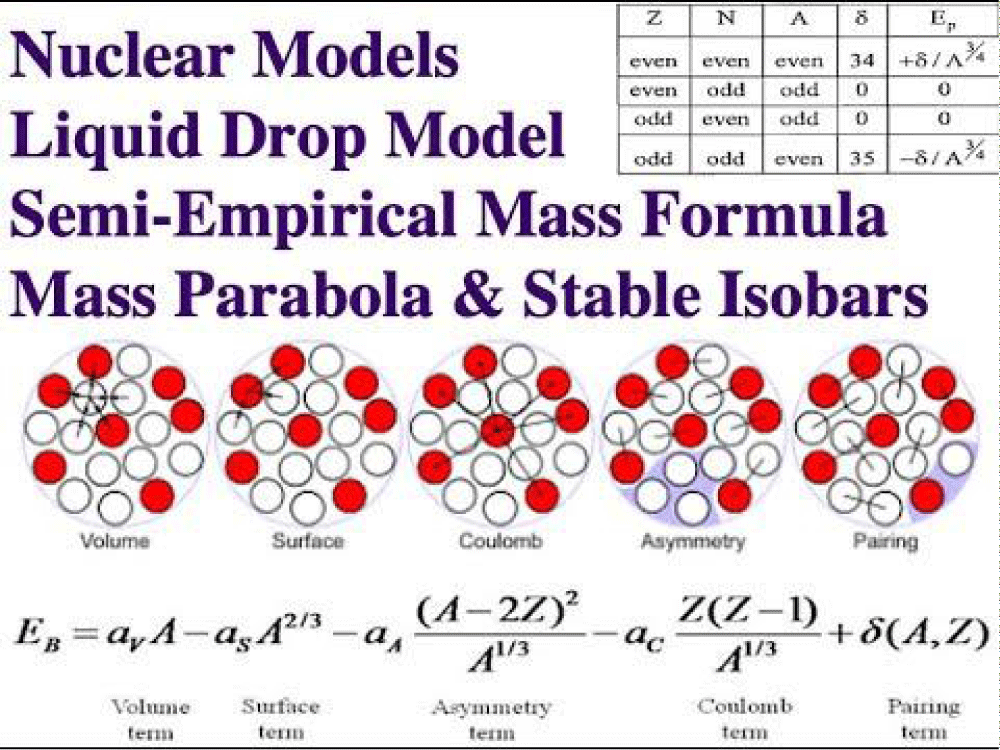
According to the fluid drop concept of the nucleus, the somewhat empirical mass equation (SE) gives the following description of the energy those bonds: ESE B (Z, N).
ESE B is equivalent to aVA − aSA (2/3) − aCZ (Z − 1)/A (1/3) − aA ((Z − N) 2)/A − δ (A, N)
Where δ (A, N) = ±aPA−1/2 for the nucleus with equal (odd) numbers of neutrons and protons and 0 for all other nuclei. To best suit the study’s data, the coefficients used are actually derived. These factors make it simple to visualize the energy of binding per nucleon (EB/A), as seen in Figure 1, as a 3D-printed energetic environment or as a movie.
Figure 1: The structure of the forces model is printed in three dimensions (left). The moving image (right) illustrates how the commonly used 2D graph matches the 3D concept.
The mathematical model’s predictions and the empirical findings for binding energy EExp B (Z, N) [5,6] may be contrasted [9].
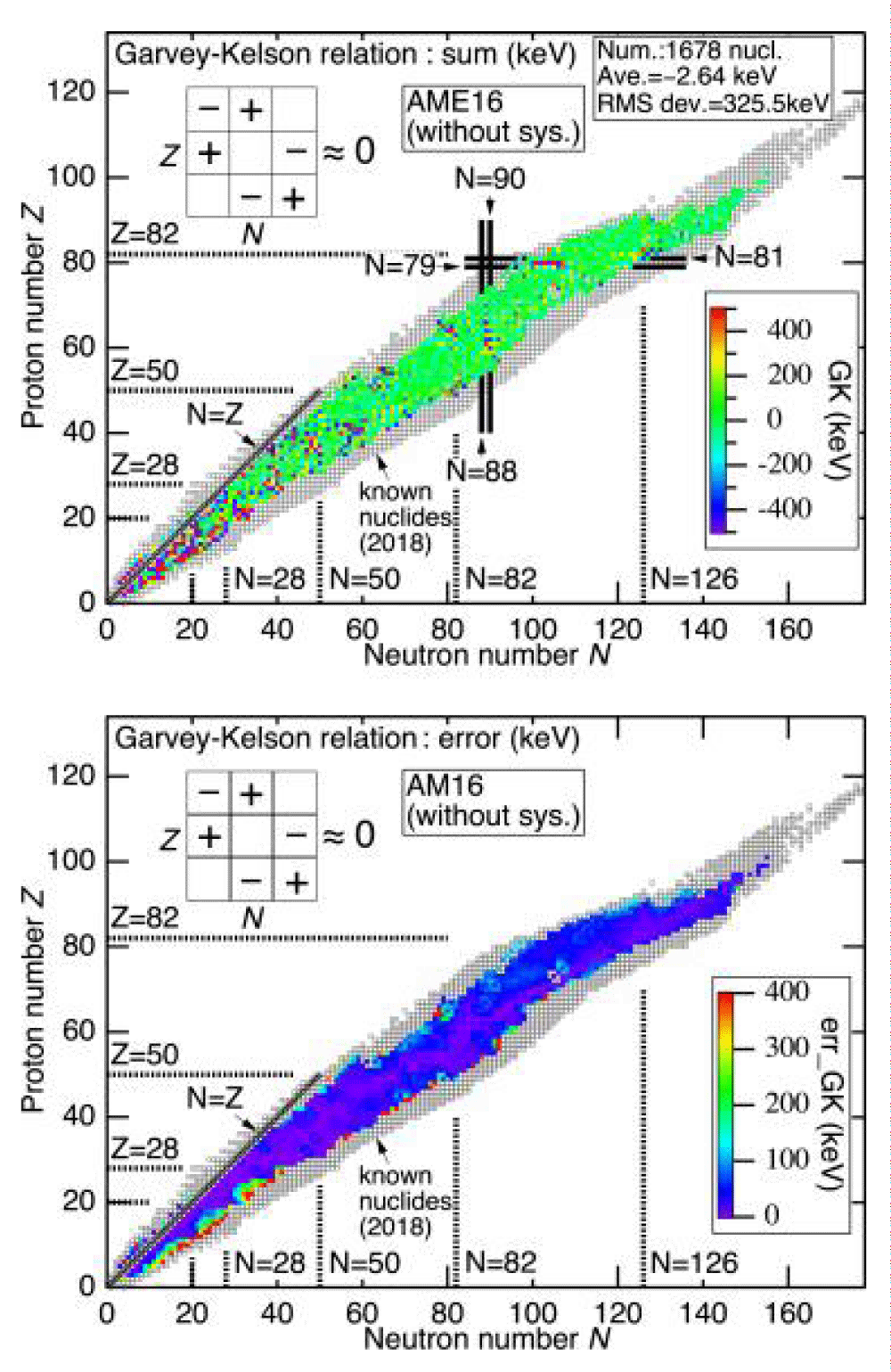
As seen in Figure 2, we prototype the variance in the potential of the binding force per nucleus, provided by Δ (Z, N) = EExp B (Z, N)/A − ESE B (Z, N)/A, for the realization as a printed in 3D object. Students may discover how to represent the water drop design’s limit of applicability by employing the model depicted in Figure 2: For tiny A, there are especially significant differences between the results of experiments and the liquid drop model [10]. For tiny A, the fundamental model premise of a circular droplet is violated. In fact, this result in a breakdown of the difference among an area term (aVA) and an area term (aSA (2/3)).
Figure 2: Duplicate digits and charm lines are shown in the difference in binding power per nucleus between the actual and SEMF data.
However, as seen in the movie and the 3D-printed model, variations get very tiny for nucleus with mystical numbers such as 2, 8, 20, 28, 50, 82, 126.... Double-magic nuclei occur when the total amount of neutrons and protons (Z, N) is equal to a magical number. The differential energy Δ (Z, N) nearly disappears at this point [11].
It is intriguing that the disparity in energy surroundings Δ(Z, N) between the experimental results and the SEMF of the energy that bonds per nucleus is capable of predicting the enchanted numbers, that have been stated within the framework of the nuclear shell model in comparison to the shell theory of the electrons that are bound that was developed by Goeppert-Mayer [12].
The basic water drop approach, first presented in 1935, does not account for the interior architecture of pearls [13]. The water drop the model’s easy presumption of a sphere-like form and disregarding inside shell details appear to be enough for the explanation of the bound energy in these kinds of cases. If the amounts of electrons and protons match the enchanted numbers, a particular amount of shells will be entirely filled.
Problem of the statement
The field of nuclear relies heavily on the largely empirical weight factor for calculating nuclear bonding strengths. It is not devoid restrictions, though. A major problem is that, although SEMF is a fair estimation, it frequently cannot forecast the binding forces of nuclei with high neutron-to-proton proportions [14]. The formula’s reliance on averaging variables, which ignore certain nucleus connections and shell effects—particularly in heavy as well as light nuclei—gives rise to this shortcoming.
Furthermore, when contrasted with actual data, SEMF’s oversimplified interpretation of the nuclear power and its constituent elements—volume, appear, Coulomb’s theory asymmetry, and coupling terms—may result in disparities. Because of these constraints, more complex models or actual modifications are required to increase nuclear predictability and strength.
In “Modeling in Radioactive Science: A Graphical Method to the Constraints of the somewhat empirical Mass The formula,” the study method focuses on improving the conventional somewhat empirical mass equation (SEMF) by visually analyzing its variables and limitations in great length. Based on a number of fundamental words that stand for various chemical forces and processes inside the cell’s nucleus, the SEMF is a fundamental model used to predict nuclear bonding strengths.
The quantity term, surface phrase, Electrostatic term, asymmetries term, and pairing term are the fundamental elements of the formula that the researchers reaffirmed before tackling the issue. Each of the above components was examined for its empirical match to available nuclear data as well as for their material importance [15].
Additionally, the research used an artistic approach to spot and fix variations in the experimental findings and SEMF forecasts. Calculating bound energy information against numbers of masses and looking for discrepancies were part of this process. Modifications were suggested via this graphical analysis to more accurately reflect factors such as shell adjustments and certain nuclear structural errors that the initial equation could miss [16]. The goal of the research was to improve the predicted accuracy of the SEMF, especially for nuclei with severe neutron-to-proton ratios (INSPIRE) (Pubs AIP), by fine-tuning the empirical variables and adding fixes [17].
In order to calculate the mass of a nucleus in an atom from the amount of neutrons and protons, nuclear physicists use the Semi-Empirical Mass Formula (SEMF), also known as the Weizsäcker formula, Bethe–Weizsäcker formula, or Bethe–Weizsäcker mass formula to distinguish it from the Bethe–Weizsäcker procedure. It is based on both theory and real-life measurements, as the name implies. The formula is a representation of Georges Gamow’s liquid-drop model, which can explain most of its components and provides approximations for the coefficients [18]. The German scientist Carl Frederick von Weizsäcker initially proposed a formula in 1935, and while the coefficients have since been improved, the formula’s general structure has remained constant.
The model represents a liquid discharge
Theodore Gamow was the first to suggest the liquid-drop model, which was further improved by the work of Niels Bohr, John Campbell Wheeler, and Lise Meitner. . There is a resemblance to the arrangement of a round liquid drop since it regards its center as a sphere of insoluble fluid of extremely high density, kept together by the force of nature (a leftover effect of the nuclear force) [19]. The liquid-drop model, albeit imprecise, provides an approximation of binding energy and takes into consideration the circular form of the majority of protons (Figure 2).
The formula
The total mass of a nucleus in an atom for neutrons, protons, and therefore nucleons that is calculated using the following formula:
,
Wherein the atom’s binding power and are the rest is masses of a proton and a neutron, accordingly [20]. The limiting energy, according to the partially empirical mass equation, is
.
This formula’s terms are all supported by theory. The coefficients 𝑎 V {\displaystyle a_{\text{V}}}, 𝑎 S {\displaystyle a_{\text{S}}}, 𝑎 C {\displaystyle a_{\text{C}}}, 𝑎 A {\displaystyle a_{\text{A}}}, and 𝑎 P {\displaystyle a_{\text{P}}} are all empirically determined; although they may be derived from experimentation [21]. Although it’s usually described by its fundamental five words, there are more names to explain other phenomena. The interaction between these coefficients when new phenomena are included is complicated; some terms impact each other, while the 𝑎 P {\displaystyle a_ {\text{P}}} term is mostly autonomous. This is similar to how altering a polynomial fit would alter its variables (Figure 3,4).
Figure 3: Shows how the variables in the liquid-drop model that represent the atomic nucleus relate to the semi-empirical mass formula..
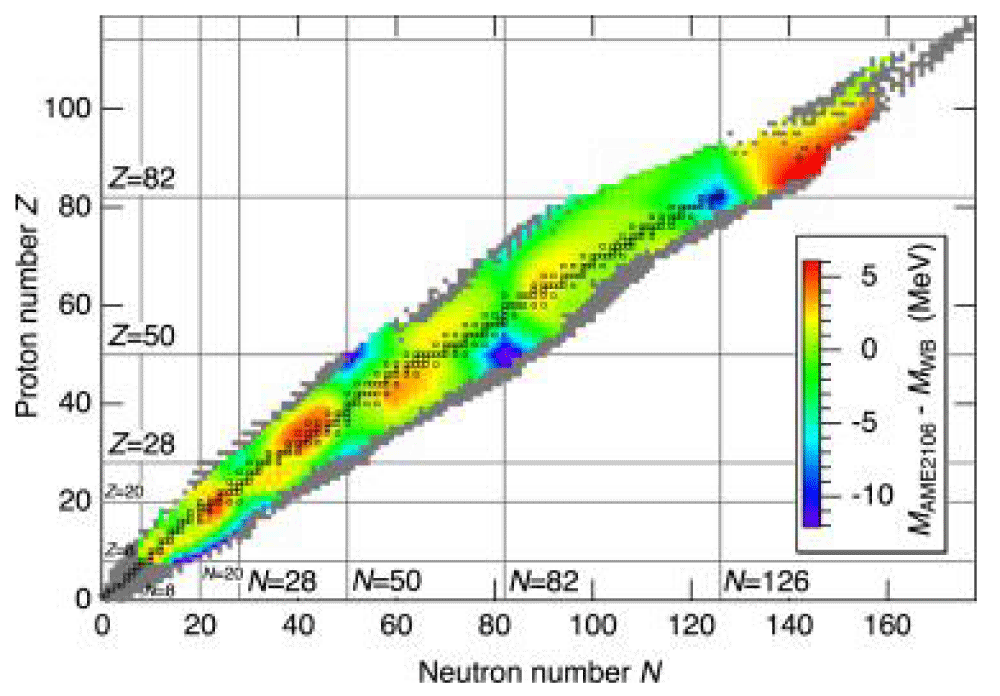
Figure 4: The bound energy per nucleus (measured in MeV) according to the semi-empirical mass calculation, as determined by the combination of the neutrons number N and the atomic number Z. Elements that have been found through experimentation are shown by a line with a dash.
Doing the coefficient calculations
Matching to empirically observed nuclei’s masses yields the coefficients. According to how well they fit the data and whatever unit is used to describe the mass, their values can change. A few of the instances are displayed below (Table 1).
| Table 1: Example of coefficient calculation. | |||||
| Unit | Eisberg & Resnick [7] | Least-squares fit (1) | Least-squares fit (2)[8] | Rohlf[9] | Wapstra |
| av | u | MeV | MeV | MeV | MeV |
| as | 0.01691 | 15.8 | 15.76 | 15.75 | 14.1 |
| ac | 0.01911 | 18.3 | 0.711 | 0.711 | 0.595 |
| aA | 0.000763[α] | 0.714 | 23.702 | 23.7 | 19 |
| ap | 0.10175[β] | 23.2 | 34 | 11.18 | 33.5 |
| kp | 0.012 | 12 | |||
| −1/2 | −1/2 | −3/4 | −1/2 | −3/4 | |
| (even-odd_odd-even) | 0 | 0 | 0 | 0 | 0 |
| ^ This model uses in the numerator of the Coulomb term. | |||||
The nucleus’s interior shell structure is not taken into account by the formula.
As a result, the semi-empirical mass equation fits heavier nuclei well while fitting very light nuclei—particularly 4He—poorly. Generally, it is preferable to adopt a model that accounts for this shell shape for light nuclei [22-24].
The semi-empirical mass formula (SEMF), which is derived from the number of protons and neutrons in an atomic nucleus, is used in nuclear physics to estimate the mass and other parameters of an atomic nucleus. It is based on both theory and actual measurements, as the name implies [25-28]. George Gamow’s liquid drop model, which can explain the majority of the formula’s components and provides ballpark estimates for the coefficient values, is the foundation of the theory.
In this work, we used an instance of radioactive physics to illustrate the features and limitations of real-world models utilizing 3D printing and animations methods. Learners are fascinated and encouraged to investigate when they are given more tactile access to the thing through printed models. This framework permits prediction of decay series in relation to decay of radioactivity. Iron is possibly the most durable element of all since it is located at the lowest point in the energetic spectrum. Fluid visualizations benefit greatly from the usage of movements. For the initial time, here, we displayed an animation contrasting the liquid’s forecasts with the various power landscapes. Drop model using real empirical information. In this sense, the unique significance of magical figures are disclosed because the SEMF’s reliability is especially high in these circumstances, whereby may be taken straight from the video and read. While a wide range of images are possible due to the fast advancements in computer graphics. For students, the nature of physical models is not immediately apparent. Consequently, fur-Empirical studies pertaining to model comprehension and its association with multiple potential. It is necessary to have representatives. We think that nuclear physics models offer an excellent illustration.
- Ubben M, Heusler S. Gestalt and functionality as independent dimensions of mental models in science Res. Sci. Educ. 2019; 49:1–15.
- Ubben M, Heusler S. A haptic model of vibration modes in spherical geometry and its application in atomic physics, nuclear physics and beyond Eur. J. Phys. 2018; 39:045404.
- Martin BR, Shaw G. Nuclear and particle physics: an introduction. 3rd ed. Hoboken, NJ: Wiley; 2019. p. 62. ISBN 978-1-119-34462-9. OCLC 1078954632.
- Oregon State University. Nuclear masses and binding energy lesson 3. Oregon State University. cited 2015 Sep 30.
- Möller P. The limits of the nuclear chart set by fission and alpha decay. EPJ Web Conf. 2016; 131:03002:1-8. doi:10.1051/epjconf/201613103002.
- Ubben M, Heusler S. Gestalt and functionality as independent dimensions of mental models in science. RSC Educ. 2021; 51:1349.
- Ubben MS, Heusler S. A haptic model of vibration modes in spherical geometry and its application in atomic physics, nuclear physics, and beyond. Eur J Phys. 2018;39(d5404).
- Discusses the limitations of the SEMF and provides a detailed visual approach to understanding these constraints (Inspire HEP).
- Explores critical models of fission and includes discussions on the liquid-drop model and its relationship to the SEMF (Inspire HEP).
- Examines mutual influences of terms in the SEMF and extends the formula with additional terms to better fit nuclear masses (Inspire HEP).
- A new semi-empirical mass formula developed to improve the accuracy of nuclear binding energy predictions (Inspire HEP).
- Focuses on high-precision nuclear mass predictions, providing insights into modern approaches for refining the SEMF (Inspire HEP).
- Provides an overview of the SEMF, its corrections, and its application to nuclear binding energy calculations (Inspire HEP).
- Machine learning approaches to nuclear physics that involve the SEMF for modeling nuclear properties (Inspire HEP).
- General description and background of the SEMF, also known as the Weizsäcker formula, including its theoretical and empirical bases (Inspire HEP).
- Binding Blocks, Department of Physics. https://york.ac.uk/physics/public-and-schools/secondary/binding-blocks/
- Pluta WJ, Chinn CA, Duncan RG. Learners’ epistemic criteria for good scientific models. J. Res. Sci. Teach. 2011; 48 486–511.
- Bailey D. Semi-empirical Nuclear Mass Formula. PHY357: Strings & Binding Energy. University of Toronto. 2011-03-31.
- Khan DA, Khan N, Ilyas N, Gul MT. Mechanisms of Stress Tolerance in Halophytic Plants. Metascience. 2024;2(2):9-16.
- Ibrar M, Rahim K, Ullah S, Gul MT. A Brief Overview On The Highly Medicinal Plant Genus Gomphrena. Metascience. 2024;2(1):84-91.
- Khan N, Ilyas N, Gul MT. Mycorrhizal Associations' Significance for Plant Nutrition. Metascience. 2024;2(2):1-8.
- Ullah I, Khan N, Gul MT. Plants' Physiological Reactions to Climate Change. Metascience. 2024;2(1):76-83.
- Wang M, Audi G, Kondev FG. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C. 2017; 41:030003.
- Wang N, Liu M, Wu XZ, et al. Surface diffuseness correction in global mass formula. Phys Lett B 2014; 734:215-219.
- Kanber HA, Alkhalidy ME. Google scholar and the scientific originality of the professor. Iraqi J Inf Technol. 2018;8(2):22-45. (in Arabic)
- Kanbar HA. Islamic Digital Library A project to Create a Digital library for the student in the Department of Holy Quran and Islamic Education Prepare. J Iraqi Univ. 2022;55(3):277-296.
- Zheng JS, Wang NY, Wang ZY, et al. Mass predictions of the relativistic mean-field model with the radial basis function approach. Phys Rev C. 2014;90:014303.
- Niu ZM, Zhu ZL, Niu YF, et al. Radial basis function approach in nuclear mass predictions. Phys Rev C. 2013;88:024325.