Case Report
Photon Absorption characteristics of some selected Enzyme Inhibitors used in Cancer Research in the Energy range 1 keV-100 GeV

Mustafa Recep Kaçal1, Hüseyin Ali Karataş2 and Ferdi Akman3*
1Giresun University, Sciences and Arts Faculty, Department of Physics, 28100 Giresun, Turkey
2Bingöl University, Sciences and Arts Faculty, Department of Physics, 12000, Bingöl, Turkey
3Bingöl University, Vocational School of Technical Sciences, Department of Electronic Communication Technology, 12000 Bingöl, Turkey
*Address for Correspondence: Dr. Ferdi Akman, Bingöl University, Vocational School of Technical Sciences, Department of Electronic Communication Technology, 12000 Bingöl, Turkey, Tel: +904262160012-4067, +904262160012-1331; Fax: +904262150788; Email: fakman@bingol.edu.tr
Dates: Submitted: 01 August 2017; Approved: 18 August 2017; Published: 21 August 2017
How to cite this article: Kaçal MR, Karataş HA, Akman F. Photon Absorption characteristics of some selected Enzyme Inhibitors used in Cancer Research in the Energy range 1 keV-100 GeV. J Radiol Oncol. 2017; 1: 060-068. DOI: 10.29328/journal.jro.1001009
Copyright License: 2017 Kaçal MR, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Mass attenuation coefficient; Effective atomic number; Effective electron density; Enzyme inhibitor
Abstract
The absorption parameters such as total mass attenuation coefficients, molecular, atomic, and electronic cross sections, effective atomic numbers and electron densities were calculated for some selected enzyme inhibitors in the photon energy range from 1 keV up to 100 GeV. The changes in the absorption parameters were interpreted with the photoelectric effect, Compton scattering and pair production processes. It is observed that the 2-Imino-1-imidazolidineacetic acid enzyme inhibitor has more radiation shielding feature when compared to other chosen enzyme inhibitors. The present investigation is anticipated to be useful for researchers studying with radiation in several fields and cancer researchers.
Introduction
Enzymes are generally proteins which catalyze chemical reactions and they play essential roles in life processes. Enzyme inhibitors decrease the ratio of an enzyme catalyzed reaction by interfering with the enzyme in some way and this effect may be persistent or transient. Enzyme inhibitors can be used as anti-tumour agents in cancer research. For example, aminoglutethimide restricts the enzyme steroid aromatase, which is related in the biosynthesis of estrogens. It is currently utilized as an effective agent for the treatment of advanced breast cancer in post menopausal women [1]. Camptothecin is an alkaloid that exhibits anti-leukemic and anti-tumour activities [2]. It is naturally obtained and it displays intense blue fluorescence under UV light. Mevinolin, which is a fungal metabolite isolated from fungus Aspergillus sp., is a strong anti-hypercholesterolemic agent. Mevinolin inhibits cell proliferation due to cell cycle arrest in a dose-dependent manner. Mevinolin diminishes the platelet aggregation, macrophage foam cell formation, and LDL oxidation and as a result of that it can significantly attenuate the atherosclerotic process [3].
The radiation are absorbed or scattered by material. The intensity of the radiation is attenuated in the process of the absorption and this process depends on the energy of the radiation and the density, atomic number, thickness and chemical structure of the absorber. The main events during the interaction of the photon with the material ate photoelectric absorption, Compton scattering and pair production. The total mass attenuation coefficient for photons of a given energy in a given matter comprises the individual contributions from the photoelectric absorption, Compton scattering and pair production processes. The total mass attenuation coefficient is a measure of probability of interactions of photons with material and it has the dimension cm2g-1. Since a series of consecutive absorption parameters are calculated from it, the total mass attenuation coefficient is an essential parameter. Using the total mass attenuation coefficient, the molecular, atomic and, electronic cross sections, effective atomic number and electron density parameters can be derived. The probability of interaction is proportional to the cross section. This description can be used for atomic, molecular and electronic cross sections. For example, the probability of interaction with molecule can be called as molecular cross section. An element is characterized by a single atomic number. But, the complex materials such as soil, plastic or biological material cannot be characterized by a single atomic number in a given energy range. The atomic number is represented by the effective atomic number in complex materials. The effective electron density is represented as the electron numbers in the unit mass. The effective atomic number and electron density change depending on photon energy. These parameters have physical significance and allow many characteristic of matter to be visualized with a number. The correct values of these parameters are important in applied science such as calculations of absorbed dose in radiotherapy, medical physics, nuclear industry, radiation physics and shielding. Many researcher and research groups have investigated the total mass attenuation coefficient, effective atomic number and electron density [4-20]. Sayyed et al. [4], calculated the effective atomic numbers and electron densities of six analgesic and anti-inflammatory drugs in the energy range 1 keV to 100 MeV. More et al. [5], determined the mass attenuation coefficients, total atomic cross sections, molar extinction coefficients, electronic cross sections, effective atomic numbers and electron densities for few nylons at 122, 356, 511, 662, 840, 1170, 1275 and 1330 keV energies. The mass attenuation coefficients, atomic and electronic cross sections, effective atomic numbers and electron densities for some enzymes, proteins, amino acids and fatty acids were measured at 122, 356, 511, 662, 1170, 1275 and 1330 keV photon energies by Gaikwad et al. [6]. Isikli and Oto [7], computed the mass attenuation coefficients, effective atomic numbers and electron densities for fourteen anti-oxidants in the energy range 1 keV- 100 GeV using the WinXCOM code. Akman et al. [8], measured the effective atomic numbers and electron densities of some selected lanthanide complexes at 13.92, 17.75, 20.78, 26.34 and 59.54 keV photon energies using a Si(Li) detector. The total mass attenuation coefficients, total molecular, atomic and electronic cross sections, effective atomic numbers and electron densities of selected narcotic drugs were calculated by Akman et al. [9], using the WinXCOM program in the energy range from 1 keV to 100 GeV. Kumar [10], calculated the effective atomic numbers and electron densities of nucleobases DNA in the energy range 1 keV-100 GeV using the WinXCOM. Akman et al. [11], investigated the chemical effect on the total mass attenuation coefficients, molecular, atomic, and electronic cross sections, effective atomic numbers and electron densities for some selected indium complexes at 59.54 keV. The effective atomic numbers and electrons densities of some selected Gd compounds were determined using the total mass attenuation coefficients in the energy range from 39.52 to 57.14 keV by Akman et al. [12]. The effective atomic numbers and electron densities from the measured values of mass attenuation coefficients for some selected samarium compounds near the K edge in the photon energy range from 36.847 up to 57.142 keV were determined by Akman et al. [13]. Kore and Pawar [14], determined the effective atomic numbers and electron densities from mass attenuation coefficients of some amino acids at 122, 356, 511, 622, 1170, 1275 and 1330 keV energies using a NaI(Tl) detector. Manjunatha [15], computed the total mass attenuation coefficients, effective atomic numbers and electron densities of some hormones in the wide energy range 1 keV-100 GeV using the WinXCOM. Manjunatha and Rudraswamy [16], calculated the effective atomic numbers and electrons densities of human organs and tissues in the energy region 1 keV to 100 GeV. Kaçal et al. [17], measured the mass attenuation coefficients of the some elements at 59.5 and 88.0 keV energies using the different three detectors. Manjunatha [18], measured the mass attenuation coefficients, effective atomic numbers, electron densities and electrical conductivities for YBa2Cu3O7 in the energy range 0.084 MeV to 1.330 MeV. Seenappa et al. [19], determined the mass attenuation coefficients, linear attenuation coefficients, half value layers and tenth value layers for barium compounds at 32, 74 and 662 keV energies. Manjunatha [20], estimated the gamma attenuation parameters such as mass attenuation coefficient, effective atomic number and electron density of poly methyl methacrylate and Kapton polyimide in the energy ranging from 84 keV to 1330 keV.
In the present work, the total mass attenuation coefficients, molecular, atomic, and electronics cross sections, effective atomic numbers and electron densities of some selected enzyme inhibitors used in cancer research were computed in the photon energy range from 1 keV up to 100 GeV using the WinXCOM program [21]. This program gives the attenuation coefficients of any matter as the sum of the appropriately weighted contributions from the individual elements.
Theoretical calculation process
For a piece of homogeneous material of finite thickness x, the absorption of the monochromatic radiation can be described by the Lambert-Beer law. According to this law, the intensity of the incident photon will be exponentially decreased. The absorption of incident photon depends on the total mass attenuation coefficient μ/ρ, the density of the matter ρ and the thickness of the matter x.
If this equation is rearranged for μ/ρ;
Where, I0 and I are primary intensity and transmitted intensity respectively, x is the thickness of the absorber and ρ is the density of the absorber. The total mass attenuation coefficient is the sum of the photoelectric, Compton scattering and pair production cross sections. They are related with average energy of Compton electron per scattered photon, energy reemitted as fluorescent radiation and annihilation radiation, respectively. The total mass attenuation coefficient (μ/ρ)(M) of a complex material M consisting of a mixture of several chemical elements, can be computed from the total mass attenuation coefficients of the n constituting elements.
Where, (μ/ρ)i is the total mass attenuation coefficient of the ith pure element and Wi its mass fraction in the sample considered. This is called the mixture rule.
The determined values of total mass attenuation coefficients were used to obtain the molecular cross sections (cm2 molecule-1).
where, (μ/ρ)comp is total mass attenuation coefficient of the complex matter, N specifies the Avogadro number, ni is the number of atom of the ith individual element and Ai is the atomic weight of the ith constituent element in given complex matter. The simple relationship between the molecular cross section and the atomic cross section is as follows.
The atomic cross section has the dimension cm2 atom-1. The electronic cross section can be computed using the following equation.
Where, fi is the fractional abundance of it element in the complex matter and Zi is the atomic number of ith element in given matter. The electronic cross section has the dimension cm2 electrons-1. The effective atomic number, which is dimensionless magnitude, is calculated from the ratio of the electronic cross section of the atomic cross section, namely.
With the help of the effective atomic number parameter, the effective electron density can be computed as follows.
In the equation, Atot is the total atomic weight or molecular weight of complex matter and ntot is the total number of atoms in complex matter. It has the dimension electrons g-1.
Results and Discussion
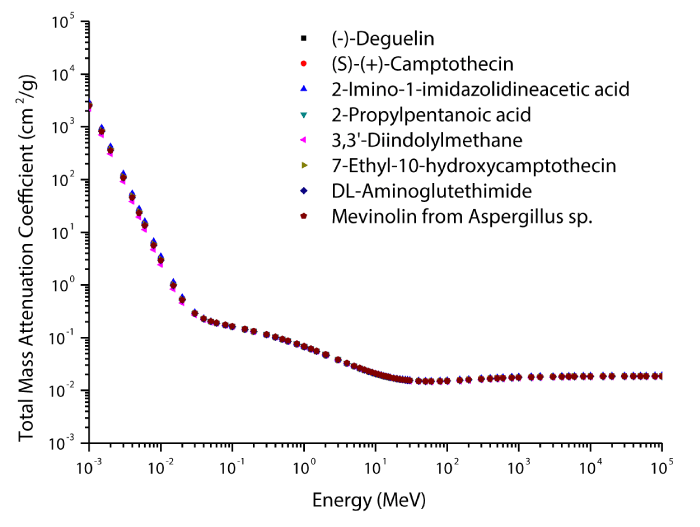
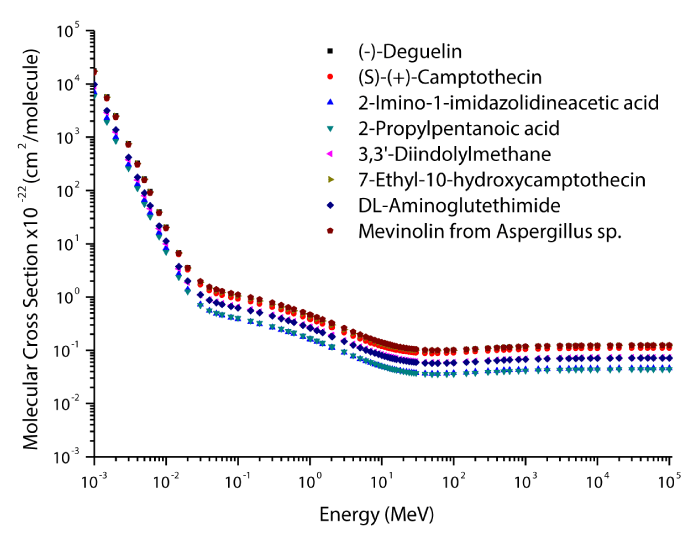
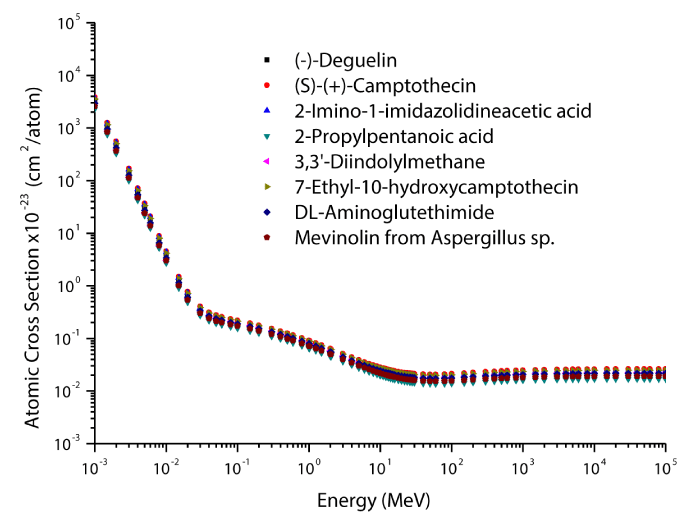
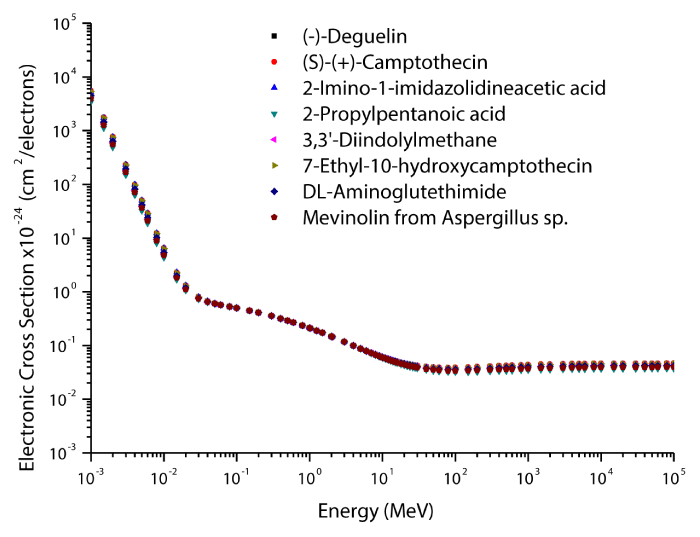
The chemical formulas and elements weight fraction of the investigated enzyme inhibitors are given in table 1. The total mass attenuation coefficients, molecular, atomic and electronic cross sections, effective atomic numbers and electron densities were obtained for some selected enzyme inhibitors. Firstly, the total mass attenuation coefficient values of selected enzyme inhibitors were obtained in the energy range 1 keV-100 GeV using the WinXCOM program. Later, using the total mass attenuation coefficient values, the molecular, atomic and electronic cross sections values were computed with the aid of the equations (4,5,6), respectively. Thereafter, the effective atomic number values were estimated with the help of the atomic and electronic cross section values using the equation (7). Finally, the effective electron density values were determined from the effective atomic number values utilizing the equation (8).
| Table 1: Chemical formulas and elements weight fraction of the investigated enzyme inhibitors. | |||||
| Enzyme Inhibitor | Chemical formula | Carbon | Hydrogen | Oxygen | Nitrogen |
| (-)-Deguelin | C23H22O6 | 0.7004 | 0.0562 | 0.2434 | |
| (S)-(+)-Camptathecin | C20H16N2O4 | 0.6316 | 0.0424 | 0.2524 | 0.0737 |
| 2-Imino-1imidazolidineacetic acid | C5H9N3O2 | 0.4195 | 0.0634 | 0.2235 | 0.2935 |
| 2-Propylpentanoic acid | (CH3CHCH2CHCH2)CH2CHCOCH2H | 0.6663 | 0.1118 | 0.2219 | |
| 3-3’-Diindolymethane | C17H14N2 | 0.8290 | 0.0573 | 0.1137 | |
| 7-Ethyl-10hydroxycamtothecin | C22H20N2O5 | 0.6734 | 0.0514 | 0.2039 | 0.0714 |
| DL-Aminoglutethimide | C13H16N2O2 | 0.6722 | 0.0694 | 0.1378 | 0.1206 |
| Mevinolin from | C24H36O5 | 0.7126 | 0.0897 | 0.1977 | |
| Aspergillussp. | |||||
The theoretical values of the total mass attenuation coefficients, molecular, atomic, and electronic cross sections, effective atomic numbers and electron densities of the Deguelin enzyme inhibitor are given in table 2. The values of total mass attenuation coefficient, molecular, atomic, and electronic cross sections are shown graphically in figures 1-4. It is clearly seen from table 2 and figures 1-4 that the total mass attenuation coefficients, molecular, atomic, and electronic cross sections depend on the energy and chemical structure of enzyme inhibitor and these parameters decrease with increasing energy. Also, these parameters decrease with increasing element number in the enzyme inhibitors.
| Table 2: The selected values of μ/ρ (cm2 g-1), σt,m (cm2 molecule-1), σt,a (cm2 atom-1), σt,e (cm2 electrons-1), Zeff and NE (electrons g-1) for Deguelin enzyme inhibitor. | ||||||
| Energy (MeV) | μ/ρ | σt,m(x10-22) | σt,a(x10-22) | σt,e(x10-22) | Zeff | NE(x1023) |
| 0.001 | 2665.850 | 17459.811 | 3423.492 | 5112.446 | 6.696 | 70.875 |
| 0.002 | 867.637 | 5682.534 | 1114.222 | 1656.637 | 6.726 | 71.187 |
| 0.002 | 381.117 | 2496.100 | 489.431 | 725.850 | 6.743 | 71.367 |
| 0.003 | 116.125 | 760.554 | 149.128 | 220.617 | 6.760 | 71.544 |
| 0.004 | 49.159 | 321.962 | 63.130 | 93.360 | 6.762 | 71.570 |
| 0.005 | 25.071 | 164.204 | 32.197 | 47.675 | 6.753 | 71.478 |
| 0.006 | 14.430 | 94.508 | 18.531 | 27.522 | 6.733 | 71.266 |
| 0.008 | 6.058 | 39.675 | 7.779 | 11.686 | 6.657 | 70.455 |
| 0.010 | 3.133 | 20.516 | 4.023 | 6.161 | 6.529 | 69.105 |
| 0.015 | 1.033 | 6.769 | 1.327 | 2.199 | 6.034 | 63.868 |
| 0.020 | 0.541 | 3.543 | 0.695 | 1.267 | 5.481 | 58.012 |
| 0.030 | 0.291 | 1.909 | 0.374 | 0.789 | 4.741 | 50.184 |
| 0.040 | 0.228 | 1.492 | 0.293 | 0.662 | 4.419 | 46.774 |
| 0.050 | 0.202 | 1.322 | 0.259 | 0.606 | 4.276 | 45.261 |
| 0.060 | 0.188 | 1.228 | 0.241 | 0.573 | 4.205 | 44.509 |
| 5.000 | 0.029 | 0.187 | 0.037 | 0.088 | 4.173 | 44.171 |
| 6.000 | 0.026 | 0.171 | 0.033 | 0.079 | 4.207 | 44.532 |
| 7.000 | 0.024 | 0.158 | 0.031 | 0.073 | 4.242 | 44.896 |
| 8.000 | 0.023 | 0.149 | 0.029 | 0.068 | 4.276 | 45.257 |
| 9.000 | 0.022 | 0.141 | 0.028 | 0.064 | 4.310 | 45.614 |
| 10.000 | 0.021 | 0.135 | 0.027 | 0.061 | 4.343 | 45.962 |
| 11.000 | 0.020 | 0.130 | 0.026 | 0.058 | 4.374 | 46.298 |
| 12.000 | 0.019 | 0.126 | 0.025 | 0.056 | 4.405 | 46.624 |
| 13.000 | 0.019 | 0.123 | 0.024 | 0.054 | 4.435 | 46.936 |
| 14.000 | 0.018 | 0.120 | 0.023 | 0.053 | 4.463 | 47.242 |
| 15.000 | 0.018 | 0.117 | 0.023 | 0.051 | 4.491 | 47.533 |
| 16.000 | 0.018 | 0.115 | 0.023 | 0.050 | 4.517 | 47.812 |
| 18.000 | 0.017 | 0.111 | 0.022 | 0.048 | 4.567 | 48.338 |
| 20.000 | 0.017 | 0.108 | 0.021 | 0.046 | 4.613 | 48.826 |
| 22.000 | 0.016 | 0.106 | 0.021 | 0.045 | 4.656 | 49.279 |
| 2000.000 | 0.018 | 0.119 | 0.023 | 0.043 | 5.399 | 57.148 |
| 3000.000 | 0.018 | 0.120 | 0.024 | 0.044 | 5.399 | 57.140 |
| 4000.000 | 0.018 | 0.121 | 0.024 | 0.044 | 5.397 | 57.126 |
| 5000.000 | 0.018 | 0.121 | 0.024 | 0.044 | 5.397 | 57.118 |
| 6000.000 | 0.019 | 0.121 | 0.024 | 0.044 | 5.396 | 57.110 |
| 8000.000 | 0.019 | 0.122 | 0.024 | 0.044 | 5.395 | 57.102 |
| 10000.000 | 0.019 | 0.122 | 0.024 | 0.044 | 5.394 | 57.094 |
| 15000.000 | 0.019 | 0.122 | 0.024 | 0.044 | 5.394 | 57.086 |
| 20000.000 | 0.019 | 0.122 | 0.024 | 0.044 | 5.393 | 57.083 |
| 30000.000 | 0.019 | 0.123 | 0.024 | 0.045 | 5.393 | 57.077 |
| 40000.000 | 0.019 | 0.123 | 0.024 | 0.045 | 5.392 | 57.071 |
| 50000.000 | 0.019 | 0.123 | 0.024 | 0.045 | 5.392 | 57.070 |
| 60000.000 | 0.019 | 0.123 | 0.024 | 0.045 | 5.392 | 57.066 |
| 80000.000 | 0.019 | 0.123 | 0.024 | 0.045 | 5.392 | 57.065 |
| 100000.000 | 0.019 | 0.123 | 0.024 | 0.045 | 5.391 | 57.063 |
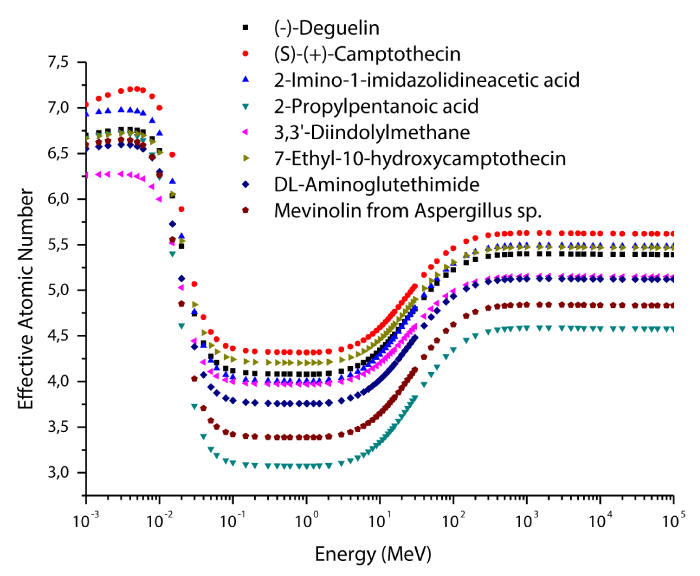
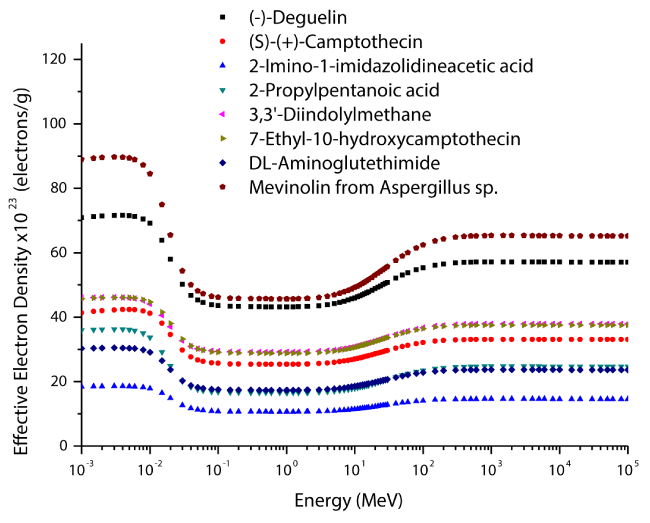
The variations of effective atomic numbers and electron densities for selected enzyme inhibitors are plotted as a function of photon energy in figures 5-6. As seen from these figures, the effective electron density shows similar behaviour to effective atomic number. It is clearly seen from figures 5-6 that the effective atomic number and electron density values are demonstrated characteristic features with respect to photon energy. According to the figures 5-6, the effective atomic numbers and electron densities decrease almost exponentially with increasing energy at low energy region. The reason for this, the photoelectric interaction dominates in this region. In general, the photoelectric effect varies with atomic number as Z4 for low energy region and Z5 for high energy region. Also, this effect changes inversely proportional with energy as E3.5. In the medium-energy region, the effective atomic numbers and electron densities take their smallest values due to Compton scattering and these values are almost constant in this region. The reason of this that Compton scattering varies with atomic number as Z, and inversely proportional with energy as E. In the high energy region, the effective atomic numbers and electron densities increase again as a function of the photon energy. The pair production interaction dominates in this region. The pair production changes with atomic number as Z2 and proportional with energy as E.
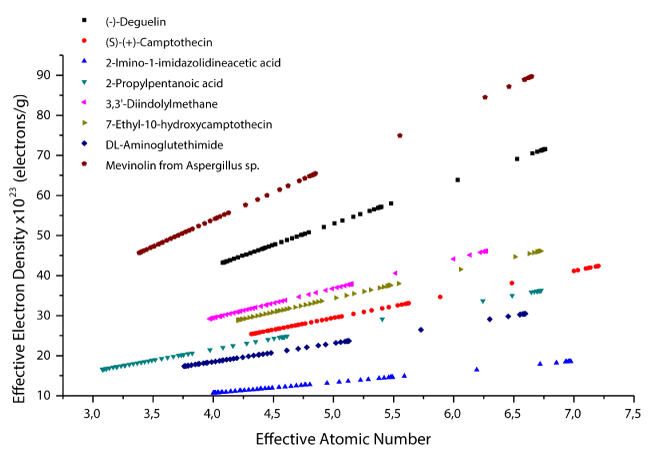
The variation of effective atomic numbers as a function of effective electron densities is given in figure 7. According to the figure 7, it is possible to say that the effective atomic number increases linearly with increasing effective electron density.
Figure 7: Effective electron densities versus effective atomic numbers of selected enzyme inhibitors.
Conclusion
We studied the changes of the total mass attenuation coefficients, molecular, atomic, and electronic cross sections, effective atomic numbers and electron densities with photon energy of some selected enzyme inhibitors. The total mass attenuation coefficients, molecular, atomic, and electronic cross sections, effective atomic numbers and electron densities depend on the photon energy, number of elements within enzyme inhibitors and chemical structure of enzyme inhibitors. The variations in the absorption parameters were interpreted with the photoelectric effect, Compton scattering and pair production processes. It can be concluded the present work that the 2-Imino-1-imidazolidineacetic acid enzyme inhibitor has more radiation shielding feature when compared to other chosen enzyme inhibitors. Study of these parameters is clear and reasonable way for evaluating extensive importance in applied areas such as cancer research, calculations of absorbed dose in radiotherapy and radiation shielding. The present investigation is anticipated to be useful for researchers studying with radiation in several fields and cancer researchers.
References
- Florey K. Analytical profiles of drug substances. Volume 15. Academic Press. 1986.
- Umezawa H. Antibiotics (Corcoran JW, Hahn FE Eds.). Springer-Verlag. 1975; 3.
- Padayatty SJ, Marcelli M, Shao TC, Cunningham GR. Lovastatin-induced apoptosis in prostate stromal cells. J Clin Endocrinol Metab. 1997; 82: 1434-1439. Ref.: https://goo.gl/PWNE2M
- Sayyed MI, Issa SAM, Auda SH. Assesment of radio-protective properties of some antiflammatory drugs. Prog Nucl Energ. 2017; 100: 297-308. Ref.: https://goo.gl/ofyNiw
- More CV, Bhosale RR, Pawar PP. Detection of new polymer materials as gamma-ray-shielding materials. Radiat Eff Def Solids. 2017; 172: 469-484. Ref.: https://goo.gl/8MUS1q
- Gaikwad DK, Pawar PP, Selvam TP. Mass ateenuation coefficients and effective atomic numbers of biological compounds for gamma ray interactions. Radiat Phys Chem. 2017; 138: 75-80. Ref.: https://goo.gl/uzksLC
- Isikli Z, Oto B. Gamma or X-rays attenuation properties of some biochemical compounds. Radiat Eff Def Solids. 2017; 172: 296-304. Ref.: https://goo.gl/iorniU
- Akman F, Kacal MR, Akman F, Soylu MS. Determination of effective atomic numbers and electron densities from mass attenuation coefficients for some selected complexes containing lanthanides. Can J Phys. 2017. Ref.: https://goo.gl/2oKQDC
- Akman F, Kacal MR, Akdemir F, Araz A, Turhan MF, et al. Calculation of absorption parameters for selected narcotic drugs in the energy range from 1 keV to 100 GeV. AIP Conference Proceedings. 2017. Ref.: https://goo.gl/xHQVji
- Kumar A. Studies on effective atomic number and electron densities of nucleobases in DNA. Radiat Phys Chem. 2016; 127: 48-55. Ref.: https://goo.gl/oZh2yY
- Akman F, Akman F, Kacal MR, Turhan MF, Akdemir F, et al. Investigation of chemical effect on the absorption parameters for some selected indium complex at 59.54 keV photon energy. Journal of Physics: Conference Series. 2016; 707. Ref.: https://goo.gl/WYBFXH
- Akman F, Durak R, Kacal MR, Bezgin F. Study of absorption parameters around the K edge for selected compounds of Gd. X-ray Spectrom. 2016; 45: 103-110. Ref.: https://goo.gl/w8gjKc
- Akman F, Durak R, Turhan MF, Kacal MR. Studies on effective atomic numbers, electron densities from mass attenuation coefficients near the K edge in some samarium compounds. Appl Radiat Isotopes. 2015; 101: 107-113. Ref.: https://goo.gl/9xasyJ
- Kore PS, Pawar PP. Measurements of mass attenuation coefficient, effective atomic number and electron density of some amino acids. Radiat Phys Chem. 2014; 98: 86-91. Ref.: https://goo.gl/En8MFw
- Manjunatha HC. A study of photon interaction in some hormones. Radiat Eff Def Solids. 2013; 168: 385-398. Ref.: https://goo.gl/ekuiQb
- Manjunatha HC, Rudraswamy B. Study of effective atomic number and electron density for tissues from human organs in the energy range of 1 keV-100 GeV. Health Phys. 2013; 104: 158-162. Ref.: https://goo.gl/pgs8bx
- Kacal MR, Han I, Akman F. Measurement of mass attenuation coefficients by Si(Li), NaI(Tl), and Cd(Tl) detectors. Nuclear Science and Technology. 2012: 59-69. Ref.: https://goo.gl/MVn9sc
- Manjunatha HC. Influence of gamma irradiation on conductivity of YBa2Cu3O7. Radiat Phys Chem. 2015; 113: 24-27. Ref.: https://goo.gl/C7YJEs
- Seenappa L, Manjunatha HC, Chandrika BM, Chikka H. A study of shielding properties of X-ray and gamma in barium compounds. J Radiat Protec Researc. 2017; 42: 26-32. Ref.: https://goo.gl/aYVwuW
- Manjunatha HC. A study of gamma attenuation parameters in poly methyl methacrylate and Kapton. Radiat Phys Chem. 2017; 137: 254-259. Ref.: https://goo.gl/hWj4Np
- Gerward L, Guilbert N, Jensen KB, Levring H. X-ray absorption in matter, reengineering XCOM. Radiat Phys Chem. 2001; 60: 23-24. Ref.: https://goo.gl/kLDMU1